
The sign in the exponent stands for a wave traveling “to the right” or toward positive z. Quite similarly we can do a position–spatial frequency transformation, i.e., a transformation between coordinate z and wave number β. The same logic applies also if instead of ω we use ω = ω − ω 0 throughout, with fixed ω 0. Then we conclude that a Fourier transform acts simply to replaceĪ factor ω in the frequency domain corresponds to an operator i( ∂/∂t) in the time domain. In the second line, we assumed that F ( t = ±∞) = 0, which means that for distant times F ( t) decays.
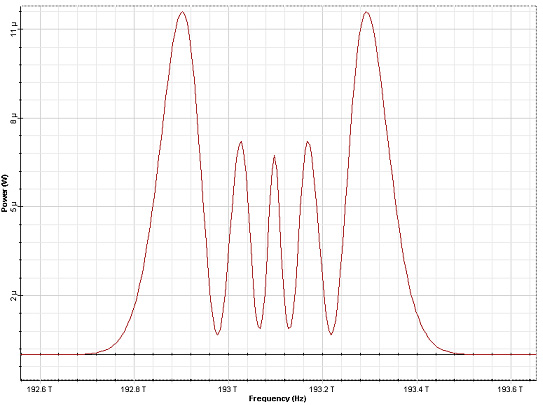
Let us begin with a time-frequency transformation of some function F ( t, z). This implies that n will now become a function of frequency (or wavelength) and power (or amplitude), and the amplitude a function of position (or distance).ĩ.3.2 Introducing Dispersion by a Fourier TechniqueĪ Fourier transform is used to convert from a function in the temporal domain to the corresponding function in the frequency domain (or vice versa), or from spatial position to spatial frequency, etc. Now we must incorporate the e ects of dispersion, loss, and nonlinearity. In a linear fiber, free from dispersion and loss, a wave packet propagates without change of shape with a velocity equal to the phase velocity. Without transverse change the pulse shape is constant. This equation describes the transverse di raction of a wave packet. So we introduce a comoving frame of reference The term containing the first temporal derivative can be scaled out. In a fiber, di raction is compensated by the waveguiding mechanism so that derivatives with respect to x and y are zero. This is di erent only in the term for transverse change. At next higher order this is what remains: Now one sees that the third and fourth term in Eq. (9.12), we note that a z derivative of A (not of E!) is the same as a t derivative up to a factor of −n/c. Indeed the equation is better than valid only in first order.
This is no wonder – we have neglected both dispersion and nonlinearity so far! This describes an envelope which propagates with constant shape and with velocity v = c/n, the phase velocity. The kth derivative is of order k 1 therefore, in leading order we only retain
The derivatives in x and y directions can be combined using the transverse nabla operator xy. Obviously the exponential factor is cancelled out, and we succeeded in finding an equation of motion for the envelope! The two terms proportional to A mutually cancel because β 0 2 = ω 0 2 n 2 /c 2.


 0 kommentar(er)
0 kommentar(er)
